Excel Sudoku Solver Code

Hello, Here is an Excel puzzle for the popular number puzzle, Sudoku. Among the most popular strategies for solving Sudoku puzzles is that of gradually eliminating all possibilities in a given. A puzzling Excel formula to help solve a Sudoku puzzle.

• • • Introduction I started trying to develop a Sudoku solver in Excel using VBA. After a few interactions with Excel, I moved to Visual Basic using VS2005. After doing a version of the program to deal with 9x9 (classic) Sudokus, I also adapted the code to solve Samurai Sudoku (5 overlapping 9x9 grids). I wanted to provide both a source and demo - as there aren't too many fully featured solvers I could find in Visual Basic to learn from.

The logic based solvers and the UI probably took the most work - the actual brute force solver was actually pretty quick to code. Terminology This article doesn't go in depth into the rules of Sudoku or the detail of how to solve Sudoku puzzles. Just use a search engine if you want background on this. However, the basic principle is that the numbers 1-9 are placed into the rows, columns, and subgrids so that every row, column, and subgrid only contain each digit once. Some terms however are used below to explain the code. • Cell - individual cell where digits 1-9 can be placed.

• Clues/givens - in the first image above, the second and third cells hold clues of 7 and 6, respectively. • Candidates/pencilmarks - in the image above, the first cell contains three candidates (2, 3, and 9). It is important when trying to solve a puzzle to keep track of the various candidates.

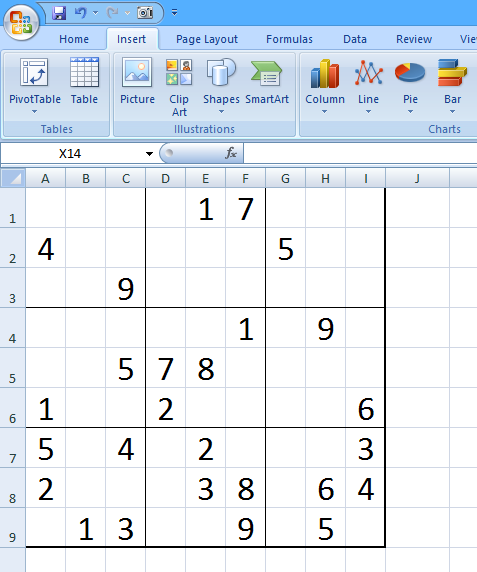
• Row - a group of 9 cells going horizontally down the screen. • Column - a group of 9 cells going vertically down the screen. • Subgrid - a group of 9 cells arranged in a 3x3 grouping. • Peers - in a 9x9 classic grid, each cell can 'see' up to 20 other cells (the other cells in the row, column, and subgrid). Due to the rule that no digit can be repeated in a row, cell, or subgrid, if you place a digit as the solution to a cell, that digit can be removed as a candidate from each of its peers.

Peers for a Samurai Sudoku are a bit different, as some cells will have a greater number of peers due to the five overlapping grids. Points of Interest The solver will try to solve puzzles using logical steps, but will also resort to a brute force algorithm for tougher puzzles. Consequently, it can solve most classic 9x9 Sudoku puzzles pretty much instantly, or most Samurai puzzles within a couple of seconds (depending on the computer). Admittedly, there are C++ solvers that can solve hundreds or thousands of puzzles per second. However, I wanted something that would solve puzzles reasonably quickly, but also be able to step through puzzles and show why particular solving steps were taken. There is a custom control which uses GDI+ to paint clues and candidates (pencilmarks). Using a bunch of individual labels or the like was far too slow to refresh.

The UI can still be a little bit slow to refresh with Samurai puzzles, but is generally not too bad. Unlike a lot of other solvers I've seen, which tend to use a two dimensional array of 81(9) to hold possible candidates for each cell, this solver uses a single array of length 81 to hold all possible candidates. Klyuch aktivacii dlya chernaya akula ii. Each candidate is assigned a value using the formula 2 ^ (candidate-1) to come up with a unique bit value for each candidate (although I've chosen to hard code this to minimise the need for this calculation). Therefore, candidate 1=bit value 1, candidate 2=bit value 2, candidate 3=bit value 4, candidate 4=bit value 8, and candidate 5=bit value 16, and so forth. 654321ROD 22-Aug-11 16:19 22-Aug-11 16:19 A well presented program with a lot of thought gone into it.